Go back to startpage
The quartic equation for time-passengers ...
.. Welcome in the year 1522 ..
Lodovico Ferrari (1522 - 1565); Italian Mathematician - born in Bologna.Unfortunately no picture of Lodovico Ferrari exists ..
Lodovico was an orphan from early childhood, and his uncle Vincenzo took care of him. However, Vincenzo saw Lodovico primarily as a burden. To rid himself of this obligation, he sent the 14-year-old Lodovico to Cardano. Since Vincenzo's son Luca was at that time serving Cardano, Vincenzo replaced Luca with Lodovico around November or December of 1536. Cardano soon recognized Lodovico's sharp mind, and because Lodovico could read and write, Cardano soon freed him from servant duties and introduced him to Latin, Greek, and mathematics. Lodovico Ferrari was the first to solve the quartic equation (under Cardano's supervision). He also supported Cardano during his famous dispute with Nicolas Tartaglia. Later, Lodovico became a wealthy man, working as a tax assessor for the governor of Milan. In 1564, Lodovico retired from his career and moved back to Bologna, his hometown, where his widowed sister Maddalena lived. Shortly after his return, Lodovico surprisingly died in 1565.
His mentor Cardano, who suspected arsenic poisoning by the greedy Maddalena (she was also the sole beneficiary), noticed that Maddalena showed no signs of grief during Lodovico's funeral. Cardano was also puzzled by the fact that no books from Lodovico's possessions were left behind. Maddalena married only two weeks after Lodovico's death, but her new husband soon left her, disappearing with all of Lodovico's inheritance. Maddalena died in poverty.
So. let's look at a quartic equation ..
One elegant approach is to rewrite both sides of the equation x4 + ax3 = - bx2 - cx - d as perfect squares. A free parameter, let's call it λ will do the job. First we add 0.25(a2x2 + λ2) + λ(x2 + 0.5*ax) to the equation. The convenient choice of λ will become any solution of the cubic equation λ3 - bλ2 + λ(ac - 4d) - c2 + 4bd - da2 = 0. As result we will obtain a product of 2 quadratic polynomials. Their solutions will become solutions of our original quartic equation.
In Q:
let be L our λ, then a2:a*a;q:((2*c)-L*a)%a2+4*L-b;A:sqrt L+(0.25*a2)-b;
Then l1:(1f,((neg A)+0.5*a),(A*q)+0.5*L) as list of length 3 and these are the coefficients of x2, x and 1.
let be L our λ, then a2:a*a;q:((2*c)-L*a)%a2+4*L-b;A:sqrt L+(0.25*a2)-b;
Then l1:(1f,((neg A)+0.5*a),(A*q)+0.5*L) as list of length 3 and these are the coefficients of x2, x and 1.
Friendly hint: Treat bi-quadratic equations and some other special trivial types separately (if you go this way), like: x4 + d = 0 or x4 + ax3 = 0.
Some examples ...
Sample 1: x4 - x - 1 = 0 : x1 = 1.220744, x2 = -0.7244919, x3,4 = -0.2481261 ± 1.033982i
Sample 2: x4 + 13x2 + 36 = 0 : x1,2 = ± 2i , x3,4 = ± 3i
Sample 3: x4 - 73x3 + 537x2 - 1115x + 650 = 0 : x1 = 1, x2 = 2, x3 = 5, x4 = 65
Sample 4: x4 + 7x3 - 38x2 + 42x - 264 = 0 : x1 = 4, x2 = -11, x3,4 = ± i*60.5
Sample 5: x4 + 2x3 + 2x2 + 10x + 25 = 0 :x1,2 = -2 ± i , x3,4 = 1 ± 2i
Sample 6:
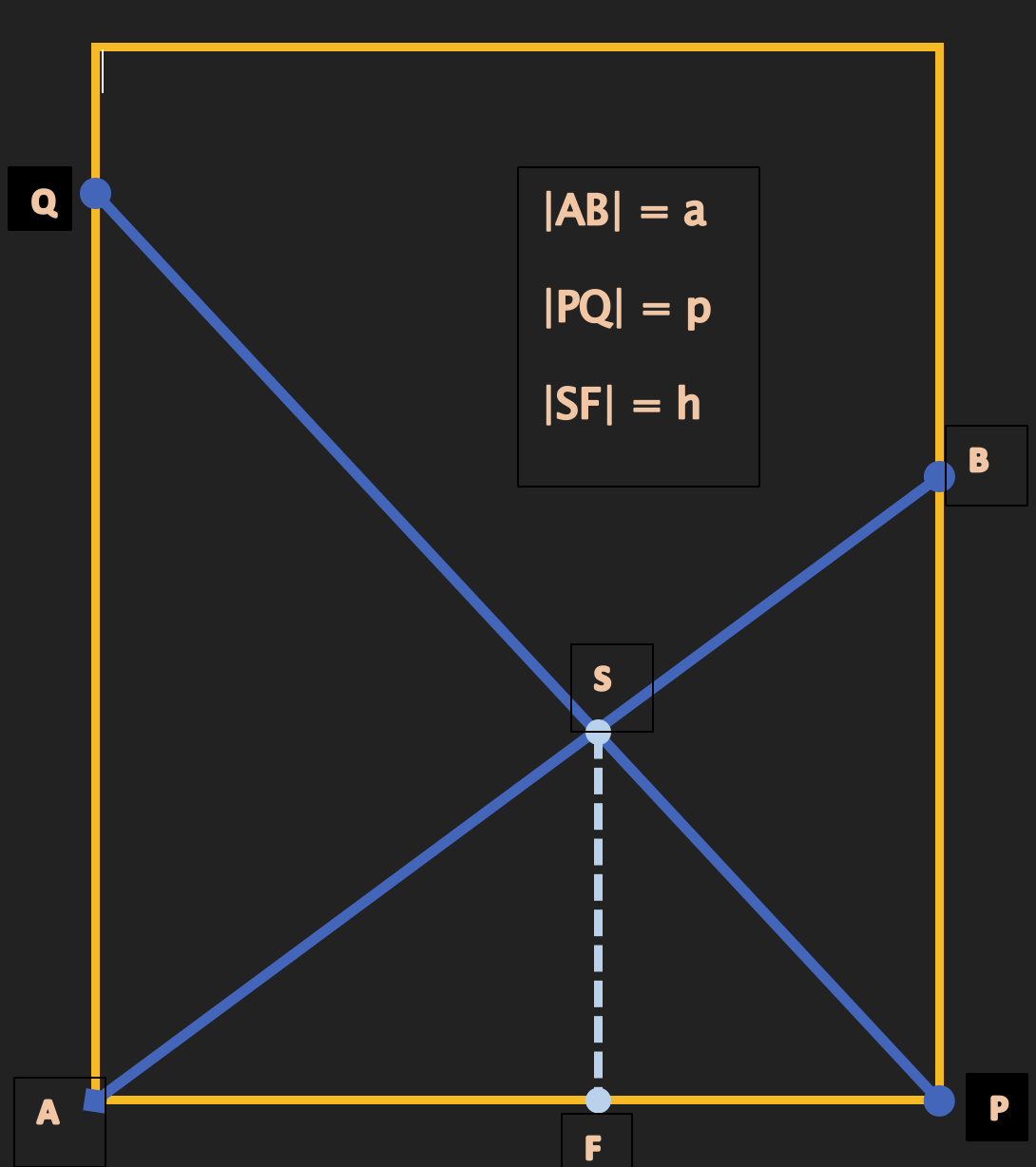
Below is a fairly common geometrical problem that leads to a quartic equation. Given the knowns a, p, and h, we are looking for the width of the rectangle, which is |AP|. Let be |AQ| = s and |PB| = t. The key to the solution is the theorem of parallel lines, which states that: h = st/(s + t). Good news for those who missed lessons on this theorem: using analytical geometry, you can derive this relationship easily. From there it is not far to the equation for t:
t4 - 2ht3 + ct2 - 2hct + ch2 = 0 (where c = a2 - b2), be aware when solving that equation is that t > h. d2 = a2 - t2
Friendly Hint: The theorem of Descartes (René Descartes, French mathematician 1596 - 1650) states that our quartic equation will have exactly two positive roots (i.e., real roots). However, in our specific problem, one of these roots will be extraneous.
Go back to startpage